XML Namespaces : Universal Identification in XML Markup
The Emperor has New Clothes : HTML Recast as an XML Application
You are here: irt.org | Articles | Markup Languages | The State of MathML : Mathematically Speaking (and Stuttering) [ previous next ]
Published on: Sunday 19th March 2000 By: Pankaj Kamthan
Since its inception in the early 1990's, the Web has become a widely accepted medium for archiving, disseminating and communicating information. In the last few years, the Web technology is moving into the arena where it can be directly useful as a tool for educational, research and commercial purposes. The development of the MathML is a major step in the direction of providing a means of [re]presenting mathematical notation on the Web.
This work examines the state of MathML, particularly the issues regarding its deployment, in the light of other technologies. The purpose of this exercise is to objectively assess the current situation with the goal to increase public awareness, rather than a marketing-oriented critique. We assume the reader has basic background in XML syntax and MathML. An elementary knowledge of some other XML vocabularies will also be useful, but is not required. For a tutorial introduction to MathML, see A Gentle Introduction to MathML.
From the very beginning, [re]presenting Mathematics on the Web proved to be a nontrivial task. In 1993, ideas for embedding Mathematics in HTML emerged in the HTML+ and subsequently in HTML 3.0 in 1994. Later, in 1996, formal support was added in HTML 3.2. However, due to lack of interest from major browser vendors, it failed to get wide acceptance.
In 1997, a Math Working Group was constituted at the World Wide Web Consortium (W3C). A solution based on Standard Generalized Markup Language (SGML) was felt to be too complicated, and it was decided that a mathematical markup language (under the name MathML) for describing mathematical content be based on XML syntax. In April 1998, MathML 1.0 Specification was announced as a W3C Recommendation, and in July 1999, it was revised to become MathML 1.01 Specification. Currently, work on MathML 2.0 is under development.
Presenting mathematics is one problem. Another problem is to search through such mathematical expressions or cut-and-paste them into computational software for further manipulation. Therefore, the markup needed to be both visually robust and meaningful. This led to the introduction of two types of markups in MathML: Presentation Markup and Content Markup.
Presentation Markup captures the notational structure of an expression. As a general rule, each presentation element corresponds to a single kind of notational "schema" such as a row, a superscript, and so on. Content Markup captures the mathematical structure of an expression. The majority of content elements correspond to a wide variety of operators, relations and named functions from topics typically found at the high school level mathematics, such as addition, square root, and so on.
Several issues have plagued widespread acceptance of MathML. They range from technical (authoring, serving, rendering), to social (public image), and to political (support). In the foregoing sections, we examine these in detail.
One comes across assertions, such as, MathML is "a simple way ... to include Math[ematics] in Web pages by hand" contrary to "it is anticipated that, in all but the simplest cases, authors will use equation editors ... to generate MathML." MathML syntax, except the most trivial cases, is verbose, and therefore naturally lends itself for machine-processing as shown in the next example.
EXAMPLE 1. The following represents Presentation and Content Markup, respectively, of the well-known Quadratic formula:
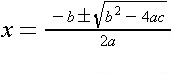 Presentation Markup (MathML source) |
 Content Markup (MathML source) |
An authoring process may involve the following steps:
This works well but only in the simple cases where one comes across a few mathematical objects in an entire document. As an example, one can use Microsoft Word for Step 1 and MathType for Step 2. However, this does not scale well with documents that contain complex mathematics, such as, theorems that mix text with mathematical expressions naturally (for an example, see here).
The approach, therefore, is not to treat mathematical objects separately in an isolated
fashion in the typographic process, but to include mathematical notation as one
"moves along" when typing. This style of authoring is common with the users of LATEX,
where an authoring "flow" is maintained by using the mathematical
"delimiters", such as, $...$ for inline and \[...\]
for display objects. This flexibility is yet to be achieved with MathML, though some
software such as the WebEQ
Wizard do provide a partial solution.
The policy "let us represent everything in MathML" just because "MathML is there" is more abuse than proper use. Use of MathML Presentation Markup for simple mathematical objects is an "overkill," since MathML markup is verbose compared to ASCII.
EXAMPLE 2. Consider the expression 1
+ sin(x). The following is the corresponding MathML Presentation Markup
for it:
<?xml version="1.0"?>
<math>
<mrow>
<mi>1</mi><mo>+</mo><mi>sin</mi><mo>⁡</mo><mo>(</mo><mi>x</mi><mo>)</mo>
</mrow>
</math>
Use of the operator element <mo> for the addition operation, and
identifier <mi> element for the Sine function, provides only
"vague" semantics. Presentation Markup is not very useful for search engines
(where it is assumed that they are searching element names and not what they
encapsulate). However, the use of MathML Content Markup may be justified, as it associates
a lot more semantics, by its very intent:
<?xml version="1.0"?> <math> <apply><plus/><cn>1</cn><apply><sin/><ci>x</ci></apply></apply> </math>
Outside the realm of W3C, almost all MathML software available is commercial. These commercial efforts also seem to be disparate, existing as independent islands of initiatives, lacking a combined major effort needed for one of the largest XML vocabularies to date. There is lack of Open Source software for authoring or translating or rendering, for MathML in general, and for MathML Content Markup, in particular. For those that are available, authoring process is made tedious by some solutions which enforce their own syntax (WebEQ and EzMath), which is translated to MathML but is incomplete. Furthermore, the rendering quality in some cases (compared to printing) is unacceptable.
There is no free lunch, and one should not be expected. But freely available and Open Source software has been one of the primary reasons for a broad utilization and success of HTML as a Web data format. The same factor is crucial for widespread adoption of XML, and in particular MathML, as well.
Elements of MathML Content Markup, which cover the basic mathematics, is too
constrained for higher-level mathematics. For example, there is no MathML Content element
to explicitly represent the "rank of a matrix operator" of Linear Algebra.
MathML allows the list of content elements to be extended (in our case, to include a
"rank of a matrix operator element") using the <annotation-xml>
element with the OpenMath encoding Content
Dictionary (in our case, BasicLinAlg) in conjunction with the <semantics>
element. However, there are cases, such as the widely-used Frobenius-Perron operator
of Ergodic Theory, where such a Content Dictionary may not exist in a specific encoding.
Without sufficient support for Content Markup, mathematical "meaning" in corresponding markup diminishes. This could be somewhat improved by appropriate use of a metadata mechanism, such as Resource Description Framework (RDF). RDF is a foundation for processing metadata. It provides interoperability between applications that exchange machine-understandable information on the Web. The RDF Syntax, based on XML, expresses and transports metadata in a manner that maximizes the interoperability of independently developed Web servers and clients. RDF Schemas define a collection of information about classes of RDF nodes, including properties and relations. RDF schemas are specified using a declarative representation language influenced by ideas from knowledge representation such as semantic nets, frames, and predicate logic, as well as database schema representation models such as binary relational models, and graph data models. A widely-used example is the Dublin Core (DC) schema.
MathML-specific metadata has not been yet formalized. However, the next example shows the utility of such an endeavour.
EXAMPLE 3. This example embeds both MathML Content Markup, and RDF markup (in serialization syntax) using the Dublin Core metadata, of the Quadratic Formula in an Extensible HyperText Markup Language (XHTML) 1.0 document:
<?xml version="1.0" encoding="UTF-8" ?> <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Strict//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-strict.dtd"> <html xmlns="http://www.w3.org/1999/xhtml" xml:lang="en" lang="en"> <head><title>Quadratic Formula</title></head> <body> <!-- RDF Description of the Quadratic Formula. --> <rdf:RDF xmlns:rdf="http://www.w3.org/1999/02/22-rdf-syntax-ns#" xmlns:dc="http://purl.org/metadata/dublin_core#"> <!-- Quadratic Formula RDF/DC Markup (within, and including the <rdf:Description> tag) here. --> </rdf:RDF> <!-- MathML Content Markup of the Quadratic Formula. --> <math xmlns="http://www.w3.org/1998/Math/MathML"> <!-- Quadratic Formula Content Markup (within, and including the <reln> tag) here. --> </math> </body> </html>
<reln> tag is being deprecated in favour of the <apply>
tag in MathML 2.0.mml in Quadratic Formula Content Markup is arbitrary. Translating the existing base of (a very large collection of) legacy documents to MathML is an important issue. Such documents are primarily in TEX (or one of its family members, such as LATEX) and Microsoft Word.
There are several questions that need to be asked (and answered to a satisfactory extent):
Even after an year and a half in existence as a W3C Recommendation, and multiple revisions thereafter, rendering support for MathML in widely-used browsers is practically nonexistent. Among freely available browsers, only the W3C test-bed browser Amaya supports almost all of the Presentation Markup. This is reminiscent of the introduction of mathematical notation in HTML 3.0 (now deprecated) which was supported only in the W3C test-bed browser Arena. The situation is improving with the MathML in Mozilla effort, but implementations are premature and the release date of Mozilla itself is unclear. Also, the current support is only for Presentation Markup.
There are browser plug-ins available, such as, IBM techexplorer Hypermedia Browser with a large support for both MathML Content and Presentation Markup. However, plug-in use suffers from historical problems such as making the browser monolithic and being a performance hog. Furthermore, it is extremely impractical approach for documents containing several mathematical objects (for an example, see here).
With MathML, we now have a mechanism of putting mathematical objects on the Web. However, there is an apparent lack of training that would lead to the realization that having mathematical notation on the Web marked-up in MathML would indeed be radically different, and useful. This situation is likely to improve as MathML enters the "consumption phase," finding its place, for example, in books and classrooms.
A widespread acceptance is necessary for any technology's widespread use. Acceptance may lead to adoption, which in turn depends strongly on public perception. Some public "misconceptions" are discussed below in detail:
As indicated in this work, there are some genuine concerns, which go beyond just misconceptions. The purpose of discussing these is to provide an objective view, rather than inflate a negative public perception, and therefore should be seen as such.
[Re]presenting mathematical notation is only part of the larger picture. This picture includes other aspects of mathematics which these notations are supposed to represent. This section discusses a few of these in detail.
Geometry plays a significant role in various areas of mathematics. Geometrical information comes into play in various ways, including the following:
Support for geometry in MathML is limited. In simple cases, such as basic commutative diagrams or other algebraic relationships, MathML could be used. Other cases, such as graphs, or geometric shapes, are beyond the scope of MathML and can not be represented. Therefore, by necessity, one has to resort to other techniques.
The issue of representing 2D geometrical structures on the Web may somewhat be resolved with the ascent of Scalable Vector Graphics (SVG). SVG is a language for "describing two-dimensional vector and mixed vector/raster graphics in XML." The next example illustrates the possibilities.
EXAMPLE 4. One simple and one complex geometrical structure represented in SVG.
Figure 1. An Ellipse (SVG source). |
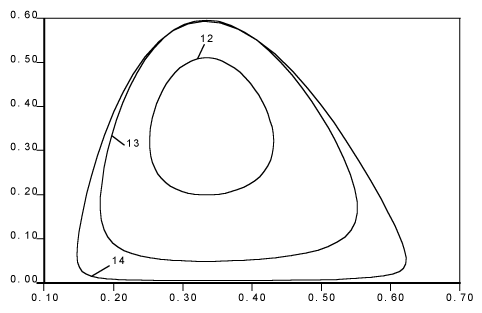 Figure 2. A Phase Plot of a system of two nonlinear ODEs |
For representing 3D geometrical structures on the Web, a different vocabulary is desirable. An important advancement in this area has been Virtual Reality Modeling Language (VRML). Inspite of the media hype, lack of native support in widely-used browsers, proprietary declarative syntax, and large file sizes, might have been some of the reasons for its limited use by general public. In the mathematical community, direct VRML authoring complex structures may be seen as inadequate (there is only so much one can do with cubes, cones and spheres). Therefore, use of mathematical software to generate these structures and subsequent translation to VRML, becomes necessary.
EXAMPLE 5.The graph of the expression
|
... (1) |
is three-dimensional in nature and can be represented in VRML (see Figure 3). MathML source for expression (1) is available.
Figure 3. A Sine function in 3D (VRML Source; 30K, Zip). |
An "XMLization" of VRML has been initiated recently under the X3D project with the goal of designing and implementing an extensible 3D graphics specification by expressing the geometry and behaviour capabilities of VRML using XML and ensuring interoperability with other standards such as XHTML, SVG and SMIL.
There are various mathematical phenomena that are dynamic in nature and need to be communicated in the form of an animation or video for a proper understanding. For example, weather data could be plotted and animated (using SMIL Animation) in SVG to show variations. Any mathematical equations involved could be represented in MathML. Such situations are common rather than an exception. The next section provides a flavour.
Iteration is an act of repeating a procedure on an object. We come across iterations everywhere. Hammering a nail, axing a log of wood, punching a number in a calculator and pressing the sin(x) button repeatedly, are all forms of iterations.
Let X be a space and f be a transformation. Then, (X,f) constitutes a dynamical system and the set {x, f(x), f2(x), ...,fn(x), where n is a nonnegative integer and x is in X} is known as a trajectory. Symbolically, we can represent the process of iteration as (a difference equation):
xn+1 = f(xn) |
... (2) |
where n=0,1,2,... can be considered as a discrete "time" variable. One of the simplest dynamical systems with complex behaviour of trajectories is ([0,1],f), when f is a one dimensional nonlinear transformation such as the Quadratic map
f(x) = a x (1 - x) |
... (3) |
where the parameter a is in the interval [0,4]. The iteration of f can be shown graphically. The value chosen corresponding to the figures are the following: a=1.0, a=2.0, a=2.5, a=3.1, a=3.5, a=3.57, a=3.7, a=3.9, and a=4.0. The initial point in each case is x=0.35. This represents the following phenomena:
Figure 4. Quadratic Map with a=3.57, x=0.35. |
Here is the demo in SMIL: Quadratic Map : Transitions from a Fixed Point to Chaos (127K, Zip). It uses media components such as RealText, RealPix and RealAudio from RealNetworks. You will therefore need RealPlayer to play the presentation.
It's about Mathematical Communication ... The Rest is Technology.
A concept or a phenomenon often requires more than one technology for its representation. A "convergence" of technologies to provide this "completeness" is therefore necessary. A significant development that facilitiates this interplay is XML Namespaces.
XML Namespaces provides a method for elements (and attributes) from different XML vocabularies to coexist coherently in the same document without any potential conflict. As the examples above have illustrated, use of MathML in conjunction with other XML vocabularies is important, and even necessary. Whether sufficient rendering support for a combination thereof is available is an entirely different matter. It poses a major challenge for the future, as the current situation is less than optimistic, perhaps more for political/commercial than for technical reasons.
MathML is a well-deserved tribute to Mathematics, the "Queen of the Sciences." However, the crowning ceremony is yet to take place. Convergence and collaboration of MathML with other technologies will be the key for a significant mathematical presence on the Web. According to the MathML 1.01 Specification, "the goal of MathML is to enable mathematics to be served, received, and processed on the Web, just as HTML has enabled this functionality for text." This goal is yet to be realized.
The RealAudio file used in the SMIL demo is by Augusto Areal. It contains a music theme composed by Giorgio Moroder for the movie Metropolis. All rights reserved. MathML authoring software MathType and WebEQ were used to generate the mathematical expressions. I would like to thank Hsueh-Ieng Pai and Martin Webb for making various editorial suggestions.
XML Namespaces : Universal Identification in XML Markup
The Emperor has New Clothes : HTML Recast as an XML Application